Summary

This paper describes an instrument devised by Joule in 1863 to detect the energy of moonlight. It is extraordinarily sensitive to heat and must convert heat into mechanical energy with high efficiency. But since the temperature rise caused by moonlight is only 10^-4 ° F, the Carnot theorem would give a maximum efficiency of 10^-6.

The thermoscope uses convection currents and involves an energy cycle at constant volume. These features form the basis of proposals I have made for the efficient conversion of solar energy into electricity that were placed on my website in March 2002, September 2002 and March 2003. Indeed Joule’s thermoscope is identical to Figure 3 in the latter Simple Solar Engine. It is my view that heat from fossil fuels or from solar energy can be converted into mechanical energy or electricity with an efficiency of up to 100% using energy cycles at constant volume.

I would be very grateful for any comments. [E-mail address:  williams.a(AT)globalwarmingsolutions.co.uk ]

Joule’s Thermoscope and the Second Law of Thermodynamics

In 1863 James Joule devised an instrument to detect the energy of moonlight^{1, 2}. It was to settle an argument with an adversary John Tyndall over whether the moon was hot or cold. He described the thermoscope as "a sort of wind thermometer"³.

I am grateful to the Museum of Science and Industry in Manchester for their efforts to track down the instrument but it does not survive nor is there any detailed drawing. The only other references found are in the introduction to a paper on the Convection Mill⁴ and in a biography of James Joule⁵.

The thermoscope is best described in a letter by Joule to his lifelong friend and colleague, William Thomson².

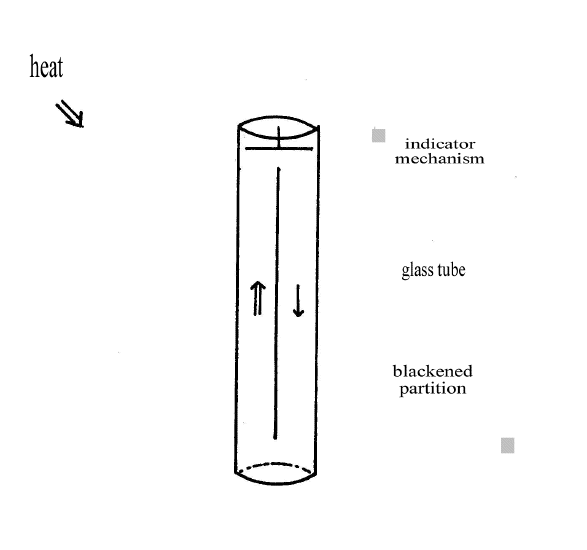
"A glass receiver 2 feet high and four inches in diameter¹ has a cardboard partition so as to divide it into two parts vertically, but leaving a space of 2 inches at the top and at the bottom. The cardboard is blackened and also two thin pieces placed in each side of the partition. It is evident that if one side is heated this least degree more than the other, the air in it will rise, descending in the other as in a bratticed coal pit shaft. The existence of such a current is made manifest by a magnetic needle an eighth of an inch long ----, furnished with a long glass index and hung by a single filament of silk.

"The delicacy of this thermoscope is such that a small blackened pan containing a pint of water heated 30° F placed at 2 yards distance makes the index go through 5° . I have increased the delicacy of the instrument by counteracting the magnetism of this earth, and now by placing it at 2 yards from a shutter with a slit in it and marking the effect of the moon as a beam of its light passes by, I find a distinct effect of about 4° which indicates, as far as I can estimate it at present, that the air on one side of this diaphragm was raised about

    1 

_____

10000 of a degree F. I intend to improve on the instrument and make it more useful by the next time we have a full moon."

Comments

The instrument devised by Joule is extraordinarily sensitive to heat – a pint of water heated 30° F placed at 2 yards produces a 5° deflection. The light of a full moon causes a 4° deflection. The energy supplied by the moon is five orders of magnitude less than that supplied by the Sun.

But the Carnot theorem tells us that the conversion of heat into mechanical energy has a maximum efficiency of D T/T. Joule¹ estimates that "the air in the instrument must have been heated by the moon’s rays a few ten thousandths of a degree." The Carnot theorem therefore gives a maximum efficiency of 10^-6.

THE CARNOT THEOREM IS WRONG

Over the decades I have always accepted the Clausius and Kelvin-Planck statements of the second law of thermodynamics. But the Carnot theorem which gives the maximum efficiency for conversion of heat into mechanical energy as D T/T has been taken by physicists to be equivalent to the second law of thermodynamics and has acquired the status of a universal law.

Clausius: It is impossible for a cyclical device to transfer heat continuously from a cold body to a hot body without the input of work or other effect on the environment.

Kelvin-Planck: It is impossible for a heat engine that operates in a cycle to convert its heat input completely into work.

The Carnot theorem gives the maximum efficiency that any heat engine could have when operating between temperatures T_H and T_L as

                                        1   -  T_L    or    DT

                                                __            __

                                                T_H           T_H

Clearly the Carnot maximum efficiency does not apply to Joule’s thermoscope. I believe it does not apply to Energy Cycles at Constant Volume6.

Joule Sensitive Thermometer 1859

Joule devised a thermometer capable of detecting temperature changes not exceeding one thousandth of a degree Fahrenheit⁷. It included a glass chimney-receiver which was sealed. Joule says, "With air in the receiver at the atmospheric pressure, the mere standing at the distance of two yards on one side of the instrument would in a short space of time cause the needle to travel through 10° in consequence of currents of air produced by the unequal heating of the walls of the glass receiver."

This again implies conversion of heat into mechanical energy with very high efficiency and in complete conflict with the predicted Carnot maximum efficiency. The instrument again involves convection currents in an energy cycle at constant volume.

Alfred R Bennett⁴ devised an instrument to demonstrate the existence of convection currents. A hollow metal cylinder painted black stands on legs inside a glass vessel which is sealed. When the instrument is placed in daylight, the metal absorbs solar energy warming air inside the cylinder which rises. It then descends in the space between the cylinder and the outer glass vessel. Vanes on the outside of the cylinder and in a window within the cylinder rotate in opposite directions demonstrating the path of convection currents. There is a Convection Mill on display in the Heat section of the Science Museum in London.

Addressing the Manchester Literary and Philosophical Society in 1897, Bennett⁸ said that, "The delicacy of the motor is such that it is affected by the radiant heat of moonlight." Bennett devised many variations of his instrument that could be used for a range of physical measurements⁴.

It is extraordinary that such an unsophisticated instrument as the Convection Mill could detect the energy of moonlight. It must mean that this extremely small amount of heat is converted into mechanical energy with very high efficiency.

But Carnot would predict a maximum conversion efficiency D T/T of about 10^-6 for moonlight.

THE CARNOT EFFICIENCY LIMIT CLEARLY DOES NOT APPLY

The instrument is another example of the use of convection currents in an energy cycle at constant volume.

All the above are examples of Energy Cycles at Constant Volume6. It is my belief that such configurations allow conversion of heat into mechanical energy with a theoretical efficiency of up to 100%. Indeed the configuration for Joule’s thermoscope is identical to Figure 3 in my proposals for a Simple Solar Engine (March 2003)⁹.

The Second Law of Thermodynamics – Limits of its Application and

The second law of thermodynamics was developed by Clausius, Rankine and Thomson 1850-1854. It tried to reconcile the work of Carnot 1820-1832 with Joule’s dynamical theory of heat 1840-1850 and the practical experience of working with steam engines. It was deeply controversial in its formulation and took over 20 years to be accepted. It has however stood the test of time. The Carnot theorem with its maximum efficiency D T/T has come to be regarded as the decisive statement of the second law of thermodynamics and has acquired the status of a universal law.

But when we look back to its founders – Joule never accepted the Carnot efficiency limit. Clausius was very hesitant about the reliability of his proof of the Carnot theorem. Rankine considered it "very unsatisfactory". No one understood Rankine’s proof. Thomson found it difficult to disagree with Joule, reluctantly accepted D T/T but wouldn’t accept Clausius’ concept of entropy. The intellectual origins of the second law of thermodynamics and its embodiment as the Carnot efficiency limit are deeply unsatisfactory.

I believe Carnot’s theorem has stood the test of time simply because the heat engines that we have produced have been very inefficient – fossil fuel power stations have an efficiency of 40%, motor vehicles 20%. We have been unable to devise machines that beat the Carnot limit.

The Carnot theorem was derived from an energy cycle where work is extracted during the expansion of a gas. All the classical thermodynamic cycles and all heat engines in operation today involve extraction of work during the expansion of a gas. In an open cycle the exhaust gases are simply discharged into the atmosphere with very large energy loss. In a closed cycle the expanded gas must be compressed to complete the cycle; the energy lost during compression goes into an energy sink. These are the sources of the inefficiency – large quantities of heat are simply dumped into the environment.

I believe there are two ways of beating the Carnot limit:

(1)  Waste Heat Recovery

Rankine¹⁰ tried to develop the ‘perfect’ air engine. He realised that the more we minimised ‘the heat which is expended in elevating the temperature of the working substance, the more nearly we shall attain to the maximum theoretical efficiency of the engine’. He suggested use of a regenerator to recycle waste heat.

In his book ‘Power Cycles and Energy Efficiency’ Hoffman¹¹ elaborates multistage compression and expansion with total waste heat recapture as the way to beat Carnot and achieve a theoretical efficiency of up to 100%.

In my proposal on the Solar Chimney – would a regenerator improve efficiency? (December 2001)¹² waste heat is infinitely recycled in a vertical heat exchanger driven by gravitation.

(2)  Energy Cycles at Constant Volume

I believe there is something extraordinary about energy cycles at constant volume. If energy is received into a closed system and work is extracted from that closed system at constant volume the theoretical efficiency is up to 100%. There is no loss of energy to an energy sink or to exit gases.

I believe that Joule’s thermoscope, Joule’s sensitive thermometer and Bennett’s Convection Mill are examples of such systems. I have devised my website entries of March 2002, September 2002 and March 2003 using such Energy Cycles at Constant Volume. Carnot’s theorem does not apply and the theoretical efficiency is up to 100%.

Dr Alan Williams                                                                                                                         July 2003

References

¹ Proceedings of the Literary and Philosophical Society of Manchester March 11^th 1863  Volume 3, p 73-4