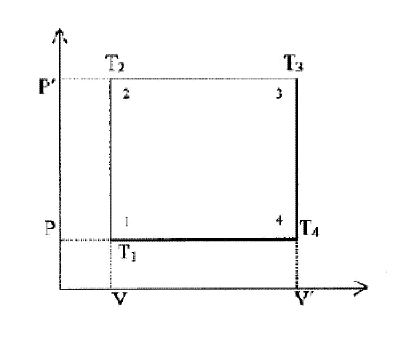
Consider the energy cycle depicted in the P-V diagram below with 2 stages at constant volume and 2 stages at constant pressure
Initial state 1 – a fixed mass of gas volume V pressure P and temperature T1
Stage 1-2 the gas is heated at constant volume to temperature T2
raising pressure to P′ Heat input Cv (T2 - T1)
Stage 2-3 the gas is heated at constant pressure to temperature T3
and volume V′ Heat input Cp (T3 - T2)
Stage 3-4 work done by gas at constant volume so that pressure
falls to P and temperature fall to T4
There is no heat input Q = DU + W = 0
work done by the gas Cv (T3 – T4)
Stage 4-1 heat taken out of the gas into energy sink at constant
pressure so that volume returns to V and temperature to T1
Efficiency = useful work achieved
total heat input
= Cv (T3 - T4)
Cv (T2 - T1) + Cp(T3 - T2)
Now consider the energy cycle portrayed approximating towards a constant volume heat engine
As V′ ® V T4 ® T1 T3 ® T2 and (T3 – T2) ® 0
Efficiency ® Cv (T2 - T1) ® 100%
Cv (T2 - T1)
If an energy cycle can be devised with the entire heat input and extraction of work at constant volume it will have a maximum theoretical efficiency of 100%.