The conversion of heat into mechanical or electrical energy is notoriously inefficient – for motor car engines 20-25%, power stations 40-50% and for solar energy using concentrators about 20% is now achievable. Such inefficiency is a consequence of the Carnot theorem.  This gives the maximum efficiency for the conversion of heat into work as DT/T where DT is the temperature rise involved and T the higher temperature in ºK.

The Carnot theorem was derived from classical thermodynamic cycles but has been elevated to the status of a universal law. Indeed it is taken to be an alternative and equivalent to the Kelvin-Planck and Clausius statements of the second law of thermodynamics. But what if there are other ways of converting heat into work? Will the Carnot theorem always apply?

All the classical thermodynamic cycles and all the heat engines used today obtain work by the expansion of a gas usually air, steam or combustion products. The pressure drives a turbine. In a closed cycle the waste product is the expanded gas which is then compressed to repeat the cycle. The compression releases a large amount of energy which is dumped in the cold temperature reservoir. Alternatively, in an open cycle, the combustion products and expanded air are released into the atmosphere.

In all cases there is a massive energy loss from the expansion of the working fluid. This is heat energy that goes into the system but is not recouped.

The ideal heat engine would operate at constant volume. Heat input would be at constant volume and work done by the gas should be at constant volume. There are some thermodynamic cycles that deploy the former – but none that employ the latter. Indeed work done is defined as PDV denoting the impossibility of extracting work at constant volume!

I don’t accept the latter and have tried to devise engines where work can be extracted at constant volume using convection currents ie gravity, as the compressor/expander. I believe that the key to the efficient generation of electricity lies in adding energy at constant volume and then feeding the warm air or combustion products into the turbine at constant volume but with raised temperature and pressure. As the fluid passes through the turbine it loses some of its velocity, pressure and temperature. This is converted into electricity with high efficiency.

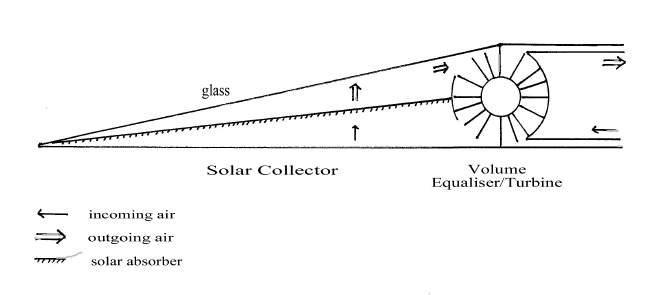
The diagrams depict a solar collector which could be from 1 square metre to 1 square kilometre in area. The solar absorber is placed symmetrically at mid level in the solar collector and is abundantly perforated to allow upward air currents. The volume equaliser has a fixed outer structure but the inner core and sectors rotate on a horizontal axis. The turbine can be placed at the core or co-axially.

Glass will allow over 90% transmittance of incident solar energy. The solar absorber also has over 90% efficiency and will produce a stream of warm air which rises. This exerts pressure on the turbine causing rotation which will introduce an exactly equal volume of ambient air at ground level into the solar collector. In this way solar energy is converted into convection currents which drive the turbine.

The solar collector operates at constant volume. Each individual sector of the annulus has identical volume. This means that the volume of air leaving the turbine per unit time will exactly equal the volume of air entering the solar collector. NO ENERGY IS LOST IN THE EXPANSION OF AIR.

The Carnot theorem tells us that if there is a temperature rise of 30ºC in the solar collector, the maximum efficiency for any heat engine is 10%.

It is my assertion however that Carnot does not apply. If there is a temperature rise of 10% at constant volume, there is a pressure rise of 10%. Turbines efficiently convert pressure into electricity. The configuration described has a simple first law efficiency. As the warm air passes through the turbine, it loses most of its velocity, pressure and temperature. It is my assertion that the theoretical efficiency for the turbine is up to 100%.

The principles outlined have been described for harnessing solar energy. Similar configurations can be devised for the combustion of fossil fuels in power stations and for continuous combustion in motor vehicle engines.

Dr Alan Williams                                                                                                                       September 2002

E-mail address:  williams.a(AT)globalwarmingsolutions.co.uk